Warum ist 1 keine Primzahl? Diese Frage beschäftigt viele Menschen, insbesondere Mathematiker. Eine Primzahl ist definiert als eine natürliche Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist. Doch die Zahl 1 erfüllt diese Bedingung nicht. In diesem Artikel werden wir den Grund dafür untersuchen und herausfinden, warum sie von der Primzahl-Definition ausgeschlossen ist.
- Wann werden Weihnachtsbäume abgeholt? Die Termine im Januar 2023.
- Cliff Richard feiert 80. Geburtstag – Wie alt ist der britische Sänger?
- Wann immer 5 Buchstaben: Ein Guide für effektive Online-Suchmaschinenoptimierung
- Leckeres Tomatenpesto einfach selbst machen!
- Einfaches Rezept für Pilzsoße selber machen – Perfekt zu Nudeln!
Warum ist 1 keine Primzahl?
Definition von Primzahlen
Eine Primzahl ist eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst.
Erfüllung der Definition
Die Zahl 1 erfüllt diese Definition nicht, da sie nur einen Teiler hat, nämlich sich selbst. Sie hat keinen weiteren Teiler außer der 1.
Konvention
Aus diesem Grund wird die Zahl 1 nicht als Primzahl betrachtet. Die Konvention besteht darin, dass Primzahlen immer größer als 1 sein müssen.
Die Eigenschaften von Primzahlen und warum 1 ausgeschlossen ist
Eigenschaften von Primzahlen:
– Eine Primzahl ist eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst.
– Primzahlen sind immer größer als 1.
– Die kleinste Primzahl ist die Zahl 2, welche auch die einzige gerade Primzahl ist.
Warum wird die Zahl 1 ausgeschlossen?
Die Zahl 1 wird als Primzahl ausgeschlossen, da sie nur einen Teiler hat (sich selbst) und somit nicht den Anforderungen einer Primzahl entspricht. Um eine eindeutige Definition für Primzahlen zu haben, werden nur Zahlen mit genau zwei Teiler als Primzahlen betrachtet.
Die Ausnahme: Warum gilt 1 nicht als Primzahl?

Grund
Die Zahl 1 wird nicht als Primzahl betrachtet, da sie nur einen Teiler hat, nämlich sich selbst. Eine Primzahl hingegen muss genau zwei Teiler haben, die Zahl selbst und die Eins. Da dies bei der Zahl 1 nicht der Fall ist, wird sie nicht als Primzahl angesehen.
Weitere Eigenschaften von Primzahlen
– Die kleinste Primzahl ist die Zahl 2.
– Alle anderen Primzahlen sind ungerade Zahlen.
– Jede gerade Zahl außer der Zahl 2 ist durch 2 teilbar und kann somit keine Primzahl sein.
– Es gibt unendlich viele Primzahlen.
Es gibt noch weitere Eigenschaften von Primzahlen, aber diese sind einige der wichtigsten. Die Zahl 1 erfüllt jedoch nicht die grundlegende Bedingung einer Primzahl und wird daher nicht zu den Primzahlen gezählt.
Warum wird die Zahl 1 nicht als Primzahl betrachtet?

Eine Primzahl ist eine besondere natürliche Zahl
Die Definition einer Primzahl besagt, dass sie genau zwei Teiler hat: die Zahl 1 und sich selbst. Die Zahl 1 erfüllt diese Bedingung nicht, da sie nur einen Teiler hat, nämlich sich selbst. Daher wird die Zahl 1 nicht als Primzahl betrachtet.
Die Eigenschaften der Zahl 1
Die Zahl 1 unterscheidet sich von den Primzahlen in mehreren Aspekten. Zum einen ist sie die kleinste natürliche Zahl und hat somit keine Vorgänger. Primzahlen hingegen haben immer mindestens eine Vorgängerzahl. Des Weiteren hat die Zahl 1 keinen eindeutigen Teiler außer sich selbst, während Primzahlen genau zwei Teiler haben.
Mathematische Konsistenz und Definitionen
Die Entscheidung, die Zahl 1 nicht als Primzahl zu betrachten, beruht auf mathematischer Konsistenz und Definitionen. Durch diese klare Unterscheidung können mathematische Aussagen und Theoreme präziser formuliert werden. Wenn man die Zahl 1 als Primzahl betrachten würde, müssten viele mathematische Konzepte und Sätze umformuliert oder neu definiert werden. Daher wird aus Gründen der mathematischen Klarheit und Eindeutigkeit die Zahl 1 nicht als Primzahl betrachtet.
Die Gründe, warum 1 keine Primzahl ist

1. Definition von Primzahlen
Eine Primzahl wird definiert als eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst. Da die Zahl 1 nur einen Teiler hat (sich selbst), erfüllt sie nicht die Definition einer Primzahl.
2. Einfluss auf die Teilbarkeit anderer Zahlen
Primzahlen haben den besonderen Charakter, dass sie nicht durch andere Zahlen außer 1 und sich selbst teilbar sind. Wenn wir die Zahl 1 als Primzahl betrachten würden, hätte dies Auswirkungen auf die Teilbarkeit anderer Zahlen. Zum Beispiel wäre jede Zahl durch 1 teilbar, was die Definition von Primzahlen verändern würde.
3. Mathematische Eigenschaften
Mathematisch gesehen hat die Zahl 1 keine eindeutigen Eigenschaften wie andere natürliche Zahlen. Sie wird oft als „leeres Element“ bezeichnet und bildet eine Ausnahme in vielen mathematischen Theorien und Regeln.
Zusammenfassend kann gesagt werden, dass die Zahl 1 keine Primzahl ist, da sie nicht die Definition einer Primzahl erfüllt und auch keine eindeutigen mathematischen Eigenschaften besitzt wie andere natürliche Zahlen.
Die Definition von Primzahlen und warum 1 ausgeschlossen ist
Definition von Primzahlen
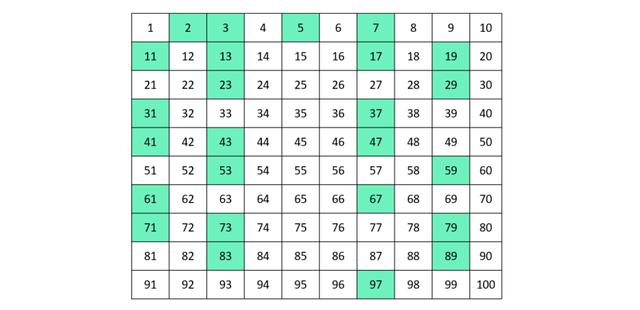
Eine Primzahl ist eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst. Das bedeutet, dass eine Primzahl nicht durch andere Zahlen ohne Rest teilbar ist. Beispiele für Primzahlen sind 2, 3, 5, 7, 11 usw.
Warum ist 1 ausgeschlossen?
Die Zahl 1 wird nicht als Primzahl betrachtet, obwohl sie nur einen Teiler hat (sich selbst). Dies liegt daran, dass die Definition von Primzahlen voraussetzt, dass eine Primzahl genau zwei Teiler haben muss. Da die Zahl 1 nur einen Teiler hat und keine weitere positive ganze Zahl ohne Rest teilen kann, wird sie nicht als Primzahl klassifiziert.
Daher beginnt die Liste der Primzahlen ab der Zahl 2.
Insgesamt zeigt sich, dass die Zahl 1 keine Primzahl ist, da sie nur einen Teiler hat und nicht den Anforderungen einer Primzahl entspricht. Es ist wichtig, diese Unterscheidung zu verstehen, um mathematische Konzepte korrekt anzuwenden und zu interpretieren.

