Einführung in Dezimalbrüche: Umwandlung & Arten

Ein Dezimalbruch ist eine mathematische Darstellung einer rationalen Zahl, bei der der Teil vor dem Komma als Ganzahl und der Teil nach dem Komma als Bruch dargestellt wird. Dezimalbrüche werden oft zur einfacheren Erfassung und Berechnung von Zahlen verwendet.

Was ist ein Dezimalbruch? Eine einfache Erklärung

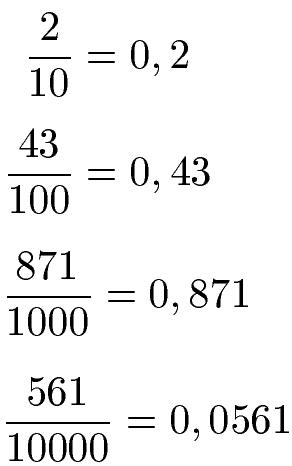
Ein Dezimalbruch ist eine spezielle Art von Bruch, bei dem der Nenner eine Potenz von 10 ist. Das bedeutet, dass im Nenner immer die Zahlen 10, 100, 1.000 und so weiter stehen. Der Zähler kann jede beliebige natürliche Zahl sein.

Um einen Dezimalbruch zu erhalten, musst du den Bruch in einen Zehnerbruch umwandeln. Dafür multiplizierst oder dividierst du den Zähler und den Nenner mit einer geeigneten Zahl, sodass im Nenner eine Potenz von 10 entsteht.

Beispiel: Angenommen du hast den Bruch 3/4 und möchtest ihn in einen Dezimalbruch umwandeln. Da der Nenner eine 4 ist, musst du ihn mit 25 (5*5) multiplizieren, um eine Potenz von 10 zu erhalten. Dadurch wird der Bruch zu 75/100. Da im Nenner zwei Nullen stehen, hat die Dezimalzahl zwei Nachkommastellen. Also entspricht der Dezimalbruch 3/4 der Dezimalzahl 0,75.

Es gibt verschiedene Arten von Dezimalbrüchen:

1. Echter Dezimalbruch: Hier steht vor dem Komma eine Null.
Beispiel: 0,2; 0,8

2. Unechter Dezimalbruch: Hier steht keine Null vor dem Komma.
Beispiel: 1,25; 14,63

3. Endlicher Dezimalbruch: Dieser Dezimalbruch kann bis auf die letzte Stelle berechnet werden.
Beispiel: 3,75; 15,2

4. Periodischer Dezimalbruch: Hier wird eine bestimmte Zahlenreihenfolge unendlich oft wiederholt.
Beispiel: 0,33333…

Das Umwandeln von Dezimalzahlen in Dezimalbrüche funktioniert ähnlich. Du schreibst die Zahl ohne Komma in den Zähler und setzt eine 1 im Nenner gefolgt von so vielen Nullen wie es Nachkommastellen gibt.

Jetzt kennst du dich bestens mit Dezimalbrüchen aus!

Dezimalbrüche verstehen: Definition und Beispiele

Ein Dezimalbruch ist ein Bruch, bei dem im Nenner eine Potenz von 10 steht, wie beispielsweise 10, 100 oder 1.000. Im Zähler kann jede natürliche Zahl stehen. Da der Nenner immer eine Zehnerpotenz ist, wird ein Dezimalbruch auch als Zehnerbruch bezeichnet.

Um einen Bruch in einen Dezimalbruch umzuwandeln, betrachtet man den Nenner und überlegt, mit welcher Zahl dieser multipliziert oder dividiert werden muss, um eine Zehnerpotenz zu erhalten. Diese Zahl wird dann sowohl für den Zähler als auch für den Nenner des Bruchs verwendet.

Eine Dezimalzahl entsteht, indem man die Anzahl der Nullen im Nenner zählt. Jede Null entspricht dabei einer Nachkommastelle in der Dezimalzahl. Zum Beispiel hat ein Nenner von 10 eine Nachkommastelle, während ein Nenner von 100 zwei Nachkommastellen ergibt.

Die Umwandlung von Kommazahlen in Dezimalbrüche funktioniert ähnlich einfach. Man schreibt die Kommazahl ohne Komma in den Zähler und setzt eine Eins als Nenner mit so vielen Nullen wie es Nachkommastellen gibt.

Es gibt verschiedene Arten von Dezimalbrüchen: echte Dezimalbrüche haben eine Null vor dem Komma, unechte Dezimalbrüche haben keine Null vor dem Komma, endliche Dezimalbrüche können bis zur letzten Stelle berechnet werden und periodische Dezimalbrüche enthalten eine bestimmte Zahlenreihenfolge, die unendlich oft wiederholt wird.

Wenn du mehr über Dezimalbrüche und deren Umwandlung erfahren möchtest, schau dir unser Video dazu an.

Einführung in Dezimalbrüche: Was du wissen solltest

Ein Dezimalbruch ist ein Bruch, bei dem im Nenner eine Potenz von 10 steht, wie zum Beispiel 10, 100 oder 1.000. Im Zähler kann jede natürliche Zahl stehen. Durch die Potenz von 10 im Nenner wird ein Dezimalbruch auch als Zehnerbruch bezeichnet.

Um einen Bruch in einen Dezimalbruch umzuwandeln, musst du den Zähler und den Nenner mit einer geeigneten Zahl erweitern oder kürzen. Dabei orientierst du dich an der Potenz von 10 im Nenner. Die Anzahl der Nullen im Nenner gibt dir die Anzahl der Nachkommastellen bei der Dezimalzahl.

Möchtest du hingegen eine Kommazahl in einen Dezimalbruch umwandeln, schreibst du die Zahl ohne Komma in den Zähler und setzt eine 1 mit entsprechend vielen Nullen als Nenner.

Es gibt verschiedene Arten von Dezimalbrüchen: echte Dezimalbrüche haben eine 0 vor dem Komma, unechte Dezimalbrüche haben keine führende Null vor dem Komma, endliche Dezimalbrüche können bis zur letzten Stelle berechnet werden und periodische Dezimalbrüche zeigen eine bestimmte Zahlenreihenfolge, die unendlich oft wiederholt wird.

Wenn du weitere Beispiele und Erklärungen zur Umwandlung von Brüchen in Dezimalzahlen sehen möchtest, schau dir unser Video dazu an.

Dezimalbrüche erklärt: Grundlagen und Anwendungen

Ein Dezimalbruch ist ein Bruch, bei dem der Nenner eine Potenz von 10 ist, wie zum Beispiel 10, 100 oder 1.000. Der Zähler kann jede natürliche Zahl sein. Durch die Potenz von 10 im Nenner wird der Dezimalbruch auch als Zehnerbruch bezeichnet.

Um einen Bruch in einen Dezimalbruch umzuwandeln, betrachtet man den Nenner und überlegt, mit welcher Zahl er multipliziert oder geteilt werden muss, um eine Potenz von 10 zu erhalten. Diese Zahl wird dann sowohl für den Zähler als auch für den Nenner angewendet.

Beispiel: Um den Bruch 3/4 in einen Dezimalbruch umzuwandeln, muss der Nenner mit 25 multipliziert werden (5 * 5 = 25). Dadurch ergibt sich der Dezimalbruch 75/100.

Umgekehrt kann man aus einem Dezimalbruch ganz einfach eine Kommazahl machen. Dazu zählt man die Nullen im Nenner und erhält dadurch die Anzahl der Nachkommastellen bei der Dezimalzahl.

Es gibt verschiedene Arten von Dezimalbrüchen, wie zum Beispiel echte Dezimalbrüche (mit einer Null vor dem Komma), unechte Dezimalbrüche (ohne Null vor dem Komma), endliche Dezimalbrüche (bei denen man alle Stellen berechnen kann) und periodische Dezimalbrüche (bei denen eine bestimmte Zahlenreihenfolge unendlich oft wiederholt wird).

Dezimalbrüche sind in vielen mathematischen Anwendungen wichtig, zum Beispiel beim Rechnen mit Geldbeträgen oder bei der Darstellung von Messwerten.

Wenn du mehr über Dezimalbrüche erfahren möchtest und Beispiele zur Umwandlung von Brüchen in Dezimalzahlen sehen möchtest, schau dir gerne unser Video dazu an.

Alles über Dezimalbrüche: Definition und Umwandlung

Ein Dezimalbruch ist ein Bruch, bei dem im Nenner eine Potenz von 10 steht, wie zum Beispiel 10, 100 oder 1.000. Der Zähler kann jede beliebige natürliche Zahl sein. Dezimalbrüche werden auch als Zehnerbrüche bezeichnet.

Um einen Bruch in einen Dezimalbruch umzuwandeln, betrachten wir den Nenner des Bruchs. Wir fragen uns, mit welcher Zahl wir den Nenner multiplizieren oder dividieren müssen, um eine Zehnerpotenz zu erhalten. Diese Zahl verwenden wir dann, um sowohl den Zähler als auch den Nenner zu erweitern bzw. zu kürzen.

Um aus einem Dezimalbruch eine Kommazahl zu machen, zählen wir die Nullen im Nenner. Jede Null entspricht einer Nachkommastelle in der Dezimalzahl. Wenn der Nenner eine 10 ist, haben wir eine Nachkommastelle. Bei einer 100 haben wir zwei Nachkommastellen und so weiter.

Die Umwandlung von Kommazahlen in Dezimalbrüche funktioniert ähnlich einfach. Wir schreiben die Zahl ohne Komma in den Zähler und setzen in den Nenner eine 1 gefolgt von so vielen Nullen wie es Nachkommastellen gibt.

Es gibt verschiedene Arten von Dezimalbrüchen:

– Echter Dezimalbruch: Eine Dezimalzahl mit einer führenden Null vor dem Komma (z.B. 0,2; 0,8).
– Unechter Dezimalbruch: Eine Dezimalzahl ohne führende Null vor dem Komma (z.B. 1,25; 14,63).
– Endlicher Dezimalbruch: Eine Dezimalzahl, die bis zur letzten Stelle berechnet werden kann (z.B. 3,75; 15,2).
– Periodischer Dezimalbruch: Eine Dezimalzahl, bei der eine bestimmte Zahlenfolge unendlich oft wiederholt wird (z.B. 0,33333…).

Das war eine kurze Einführung in Dezimalbrüche und ihre Umwandlung. Wenn du mehr darüber erfahren möchtest oder lernen möchtest, wie man mit Kommazahlen rechnet, schau dir unser Video zum Dividieren von Dezimalzahlen an!

Dezimalbrüche einfach erklärt: Grundlagen und Beispiele

Dezimalbrüche sind eine spezielle Form von Brüchen, bei denen der Nenner eine Potenz von 10 ist. Das bedeutet, dass unten im Nenner entweder 10, 100, 1.000 usw. steht. Der Zähler kann jede beliebige natürliche Zahl sein.

Um einen Bruch in einen Dezimalbruch umzuwandeln, musst du den Nenner so erweitern oder kürzen, dass eine Zehnerpotenz entsteht. Dazu multiplizierst oder dividierst du den Zähler und den Nenner mit einer bestimmten Zahl.

Wenn du aus einem Dezimalbruch eine Kommazahl machen möchtest, zählst du die Nullen im Nenner. Die Anzahl der Nullen entspricht dann der Anzahl der Nachkommastellen bei der Dezimalzahl.

Es gibt verschiedene Arten von Dezimalbrüchen. Ein echter Dezimalbruch ist eine Dezimalzahl mit einer 0 vor dem Komma (z.B. 0,2). Ein unechter Dezimalbruch hat keine 0 vor dem Komma (z.B. 1,25). Ein endlicher Dezimalbruch ist eine Dezimalzahl, die bis auf die letzte Stelle berechnet werden kann (z.B. 3,75). Ein periodischer Dezimalbruch ist eine Dezimalzahl, bei der eine bestimmte Zahlenreihenfolge unendlich oft wiederholt wird (z.B. 0,33333…).

Wenn du mehr über das Umwandeln von Brüchen in Dezimalzahlen erfahren möchtest, schau dir unser Video dazu an. Und wenn du wissen willst, wie man mit Kommazahlen rechnet, schau dir unser Video zum Dividieren von Dezimalzahlen an.

Ich hoffe, diese Erklärung hat dir geholfen, die Grundlagen der Dezimalbrüche zu verstehen.

Ein Dezimalbruch ist eine Darstellung einer rationalen Zahl, bei der der Bruchteil durch eine dezimale Ziffernfolge ausgedrückt wird. Dezimalbrüche sind in unserem Alltag weit verbreitet und leicht zu handhaben, da sie auf dem Zehnersystem basieren. Sie ermöglichen genaue Berechnungen und haben vielfältige Anwendungen in verschiedenen wissenschaftlichen und mathematischen Bereichen.