„Dividieren ist ein mathematischer Begriff, der das Teilen von Zahlen oder Größen beschreibt. In diesem Artikel werden wir die Bedeutung und die grundlegenden Regeln des Dividierens erklären. Erfahren Sie, wie Sie mithilfe dieser mathematischen Operation Zahlen effektiv teilen können.“
Die Bedeutung des Begriffs „Dividieren“ und seine Anwendung
Definition des Begriffs „Dividieren“
Beim Dividieren handelt es sich um eine der vier Grundrechenarten in der Mathematik. Dabei wird eine große Zahl, der Dividend, durch eine kleinere Zahl, den Divisor oder Teiler, geteilt. Das Ergebnis dieser Division wird als Quotient bezeichnet.
Anwendung des Dividierens
Das Dividieren wird verwendet, um verschiedene mathematische Probleme zu lösen. Es kann zum Beispiel eingesetzt werden, um Aufgaben mit großen Zahlen zu lösen, bei denen das kleine Einmaleins nicht ausreicht. Durch das schriftliche Dividieren kann man schnell und effizient zu einer Lösung gelangen.
Darüber hinaus ist das Dividieren auch wichtig für die Division mit Rest und die Division von Kommazahlen. Diese fortgeschrittenen Themen bauen auf dem schriftlichen Dividieren auf und erfordern ein fundiertes Verständnis der Grundlagen.
Insgesamt ist das Dividieren eine grundlegende Fähigkeit in der Mathematik, die es ermöglicht, komplexe Probleme zu lösen und mathematische Zusammenhänge besser zu verstehen.
Was bedeutet es, Zahlen zu dividieren?
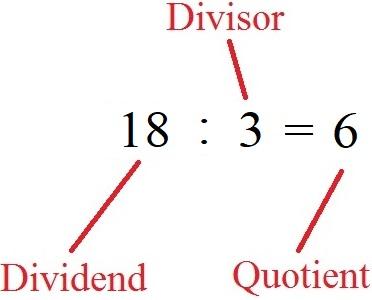
Dividieren ist eine der vier Grundrechenarten und bezeichnet das Teilen einer Zahl (Dividend) durch eine andere Zahl (Divisor), um den Quotienten zu erhalten. Beim schriftlichen Dividieren wird diese Methode verwendet, um große Zahlen auf dem Papier zu teilen.
Schriftliches Dividieren ohne Rest
Beim schriftlichen Dividieren ohne Rest teilst du den Dividend Schritt für Schritt durch den Divisor, bis du das gewünschte Ergebnis erhältst. Dabei musst du das Einmaleins beherrschen und auch schriftlich subtrahieren können.
Schriftliches Dividieren mit Rest
Falls die Division nicht aufgeht, also ein Rest bleibt, kannst du trotzdem das Ergebnis angeben. Du teilst den Dividend so oft wie möglich durch den Divisor und notierst den Quotienten. Den verbleibenden Rest gibst du ebenfalls an.
Schriftliches Dividieren mit Kommazahlen
Mit derselben Methode des schriftlichen Dividierens kannst du auch Kommazahlen dividieren. Hierbei setzt du das Komma im Ergebnis, sobald du beim Komma des Dividenden angelangt bist. Wenn sich dabei eine Schleife bildet und die Ziffern wiederholen, trägst du die Periode im Ergebnis ein.
Eine einfache Erklärung für den Begriff „Dividieren“
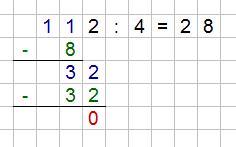
Dividieren ist eine mathematische Operation, bei der eine Zahl durch eine andere geteilt wird. Dabei wird die zu teilende Zahl als Dividend bezeichnet und die Zahl, durch die geteilt wird, als Divisor oder Teiler. Das Ergebnis dieser Division nennt man Quotient.
Beispiel: Wenn wir die Zahl 10 durch 5 dividieren, erhalten wir einen Quotienten von 2. Das bedeutet, dass die Zahl 5 genau zweimal in die Zahl 10 passt.
Manchmal geht eine Division nicht auf und es bleibt ein Rest übrig. In diesem Fall spricht man von einer Division mit Rest. Zum Beispiel lässt sich die Zahl 11 nicht genau durch 5 teilen. Hier ergibt sich ein Quotient von 2 und ein Rest von 1.
Wie funktioniert die Division von Zahlen?
Die Division von Zahlen ist eine der vier Grundrechenarten. Bei der Division teilt man eine große Zahl, den Dividend, durch einen kleineren Teiler und erhält das Ergebnis, den Quotienten. Beispielsweise ergibt die Division von 28 durch 4 den Quotienten 7.
Beim schriftlichen Dividieren wird der Dividend Schritt für Schritt durch den Teiler geteilt, bis das gewünschte Ergebnis erreicht ist. Dabei werden die einzelnen Ziffern des Dividenden nacheinander betrachtet und durch den Teiler geteilt. Dies geschieht in vier Schritten: teilen, multiplizieren, subtrahieren und verschieben.
Es ist wichtig, das Einmaleins zu beherrschen und schriftlich subtrahieren zu können, um erfolgreich schriftlich dividieren zu können. Mit dieser Methode kann man auch Divisionen mit Rest oder Kommazahlen durchführen.
Um die schriftliche Division besser zu verstehen, kann man sich anhand eines Beispiels anschauen. Nehmen wir die Aufgabe 5727 : 3. Zuerst wird die erste Ziffer des Dividenden (5) durch den Teiler (3) geteilt. Da dies nicht aufgeht, wird die nächste Ziffer (7) hinzugenommen und es ergibt sich eine 17 als Ergebnis. Dann wird dieses Ergebnis mit dem Teiler multipliziert (17 * 3 = 51) und von der ersten Ziffer des Dividenden (5) subtrahiert (5 – 5 = 0). Die nächste Ziffer des Dividenden (7) wird nach unten rechts neben das Ergebnis der Subtraktion geschrieben und der Prozess wird wiederholt. Am Ende ergibt sich das Ergebnis 1909.
Das schriftliche Dividieren kann auch bei Divisionen mit Rest oder Kommazahlen angewendet werden. Bei Divisionen mit Kommazahlen muss man darauf achten, dass man aufhört, wenn man bei der Null angelangt ist. Wenn sich dabei eine Schleife bildet, handelt es sich um ein periodisches Ergebnis.
Die schriftliche Division ist eine wichtige Methode, um große Zahlen zu dividieren und kann auch als Grundlage für die Polynomdivision dienen. Es ist von Vorteil, das schriftliche Dividieren zu beherrschen, da es einem hilft, ganze Verfahren zu lernen und fehlerfrei rechnen zu können.
Das Konzept der Division und wie man es anwendet
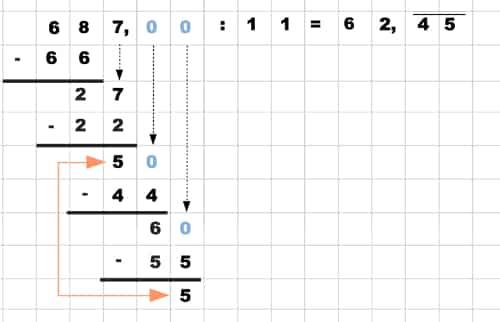
Die Division ist eine der vier Grundrechenarten. Beim Dividieren oder Teilen teilt man eine große Zahl, den Dividend, durch einen Divisor oder Teiler und erhält das Ergebnis, den Quotienten. Beispielsweise ergibt die Division von 28 durch 4 den Quotienten 7.
Beim schriftlichen Dividieren geht es darum, große Zahlen auf dem Papier zu teilen. Diese Methode ist besonders nützlich bei Divisionsaufgaben, bei denen der Dividend weit über das kleine Einmaleins hinausgeht. Um schriftlich dividieren zu können, sollte man das Einmaleins beherrschen und auch schriftlich subtrahieren können.
Das schriftliche Dividieren basiert darauf, dass man den großen Dividend Schritt für Schritt durch den Teiler teilt, bis man das gewünschte Ergebnis erhält. Dabei gibt es verschiedene Schritte wie „teilen“, „multiplizieren“, „subtrahieren“ und „verschieben“. Das Schema der schriftlichen Division hilft dabei, die Aufgabe strukturiert zu lösen.
Es gibt auch spezielle Fälle beim schriftlichen Dividieren. Wenn die erste Ziffer des Dividenden kleiner als der Teiler ist, nimmt man einfach die nächste Ziffer hinzu und teilt dann diese Zahl durch den Teiler. Auch beim schriftlichen Dividieren mit Kommazahlen kann dieselbe Methode angewendet werden.
Die schriftliche Division ist nicht nur wichtig, um große Zahlen zu teilen, sondern auch um Divisionen mit Rest oder Kommazahlen durchzuführen. Außerdem bildet sie die Grundlage für fortgeschrittenere Themen wie die Polynomdivision. Es ist daher wichtig, das schriftliche Dividieren zu beherrschen und damit sicher rechnen zu können.
Eine verständliche Erklärung für das Teilen von Zahlen
Was ist schriftliches Dividieren?
Schriftliches Dividieren ist eine Methode, um große Zahlen auf dem Papier zu teilen. Dabei teilt man eine große Zahl (den Dividend) durch einen anderen Wert (den Divisor oder Teiler) und erhält das Ergebnis (den Quotienten). Diese Methode wird verwendet, wenn der Dividend über das kleine Einmaleins hinausgeht.
Wie funktioniert schriftliches Dividieren ohne Rest?
Beim schriftlichen Dividieren ohne Rest geht man folgendermaßen vor: Man beginnt mit der ersten Ziffer des Dividenden und teilt diese durch den Teiler. Das Ergebnis wird rechts neben das Gleichheitszeichen geschrieben. Dann multipliziert man dieses Ergebnis mit dem Teiler und subtrahiert es vom Dividend. Die nächste Ziffer des Dividenden wird nach unten rechts neben das Ergebnis der Subtraktion geschrieben. Dieser Vorgang wird solange wiederholt, bis alle Ziffern des Dividenden abgearbeitet sind. Das Endergebnis ist dann der Quotient.
Wie funktioniert schriftliches Dividieren mit Rest?
Wenn die Division nicht ohne Rest aufgeht, kann man trotzdem das Ergebnis angeben. Man führt die Division wie gewohnt durch und notiert den Quotienten. Der Rest wird als Bruchteil hinter dem Quotienten notiert.
Wie funktioniert schriftliches Dividieren mit Kommazahlen?
Das schriftliche Dividieren mit Kommazahlen erfolgt nach dem gleichen Prinzip wie das Dividieren ohne Rest. Man teilt die Zahlen schrittweise und notiert das Ergebnis mit dem Komma an der richtigen Stelle. Wenn man beim Komma des Dividenden angelangt ist, setzt man auch im Ergebnis ein Komma. Es kann vorkommen, dass man in eine Schleife gerät und das Ergebnis periodisch wird. In diesem Fall trägt man die Periode im Ergebnis ein.
Welche Voraussetzungen gibt es für schriftliches Dividieren?
Um schriftliches Dividieren durchführen zu können, sollte man das Einmaleins beherrschen und schriftlich subtrahieren können. Diese Grundlagen sind wichtig, um die Division korrekt durchzuführen.
Warum ist schriftliches Dividieren wichtig?
Schriftliches Dividieren ist eine wichtige Methode in der Mathematik, um große Zahlen zu teilen. Es ermöglicht es uns, komplexe Aufgaben effizient zu lösen und mathematische Probleme zu verstehen. Durch schriftliches Dividieren können wir auch komplexere Divisionen mit Rest oder Kommazahlen durchführen.
Diese Methode hilft uns nicht nur bei der Lösung von mathematischen Aufgaben, sondern fördert auch unser logisches Denken und unsere Fähigkeit zum Problemlösen.
Zusammenfassend kann gesagt werden, dass das Teilen oder Dividieren eine grundlegende mathematische Operation ist, bei der eine Zahl in gleich große Teile aufgeteilt wird. Es ermöglicht uns, Quotienten zu berechnen und Verhältnisse zwischen Zahlen zu verstehen. Das Verständnis des Dividierens ist daher von großer Bedeutung für den Mathematikunterricht und den Alltag.

