In der Mathematik gibt es eine Regel: Eine Primzahl ist eine natürliche Zahl größer als 1, die nur durch 1 und sich selbst ohne Rest teilbar ist. Doch warum wird die Zahl 1 nicht als Primzahl betrachtet? Erfahren Sie in diesem Artikel, warum 1 keine Primzahl ist und welche Eigenschaften sie von den anderen Primzahlen unterscheidet.
- Wie viel Zwiebel ist giftig für Hunde?
- Erdmiete selber bauen: Schritt für Schritt zur eigenen Vorratsgrube
- Neueste Ereignisse in Chemnitz und Umgebung: News aus Limbach-Oberfrohna, Flöha und Frankenberg auf einen Blick!
- Rolf Zuckowski: Text von ‚Wie schön, dass du geboren bist‘
- Bundesliga 23/24 startet am 18. August 2023
Warum ist die Zahl 1 keine Primzahl?

Definition von Primzahlen
Eine Primzahl ist eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst. Das bedeutet, dass sie nicht durch andere Zahlen ohne Rest teilbar ist.
Erfüllt die Zahl 1 diese Bedingungen?
Die Zahl 1 erfüllt diese Bedingungen nicht. Sie hat nur einen Teiler, nämlich die 1 selbst. Da eine Primzahl jedoch genau zwei Teiler haben muss, kann die Zahl 1 keine Primzahl sein.
Warum ist das so?
Die Definition von Primzahlen basiert auf der Eigenschaft, dass sie nur durch sich selbst und die Zahl 1 ohne Rest teilbar sind. Die Zahl 1 erfüllt diese Eigenschaft jedoch nicht, da sie nur einen Teiler hat. Daher wird sie nicht als Primzahl betrachtet.
Zusammenfassend kann man sagen, dass die Zahl 1 keine Primzahl ist, da sie nicht den Kriterien einer Primzahl entspricht.
Die Zahl 1 und ihre Besonderheit als keine Primzahl
Die Zahl 1 ist keine Primzahl
Die Zahl 1 hat nur einen Teiler, nämlich die 1 selbst. Eine Primzahl hingegen hat genau zwei Teiler, die 1 und sich selbst. Daher wird die Zahl 1 nicht als Primzahl betrachtet.
Warum ist die Zahl 1 keine Primzahl?
Die Definition einer Primzahl besagt, dass sie genau zwei Teiler haben muss. Da die Zahl 1 nur einen Teiler hat, erfüllt sie nicht diese Bedingung und wird daher nicht als Primzahl angesehen.
Weitere Eigenschaften der Zahl 1
Die Zahl 1 ist eine besondere natürliche Zahl, da sie weder eine Primzahl noch eine zusammengesetzte Zahl ist. Sie wird auch als Einheit bezeichnet und bildet das neutrale Element bezüglich der Multiplikation. Das bedeutet, dass jedes andere Element mit der Zahl 1 multipliziert gleich dem Ausgangselement ist.
Warum wird die Zahl 1 nicht als Primzahl betrachtet?
Die Definition einer Primzahl
Eine Primzahl ist definiert als eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst. Die Zahl 1 erfüllt diese Definition jedoch nicht, da sie nur einen Teiler hat. Sie kann nur durch 1 geteilt werden und nicht durch eine andere natürliche Zahl. Daher wird die Zahl 1 nicht als Primzahl betrachtet.
Gründe für das Ausschließen der Zahl 1
Es gibt mehrere Gründe, warum die Zahl 1 nicht als Primzahl betrachtet wird:
– Konsistenz: Die Definition einer Primzahl basiert auf der Eigenschaft, dass sie genau zwei Teiler hat. Wenn man die Zahl 1 als Primzahl betrachten würde, müsste man diese Definition ändern und es wäre keine konsistente Klassifizierung mehr.
– Eindeutigkeit: Durch das Ausschließen der Zahl 1 bleibt die Klassifizierung von Primzahlen eindeutig. Jede andere natürliche Zahl kann entweder als Primzahl oder als zusammengesetzte Zahl klassifiziert werden, je nachdem, ob sie genau zwei Teiler hat oder nicht.
– Mathematische Eigenschaften: Die Eins besitzt mathematische Eigenschaften, die sie von den anderen Zahlen unterscheiden. Zum Beispiel ist jede natürliche Zahl größer als eins entweder prim oder zusammengesetzt. Diese Eigenschaft würde verloren gehen, wenn man die Eins als Primzahl betrachten würde.
Daher wird aus diesen Gründen die Zahl 1 nicht als Primzahl betrachtet.
Die Gründe, warum die Zahl 1 keine Primzahl ist

1. Definition von Primzahlen
Eine Primzahl ist definiert als eine natürliche Zahl, die genau zwei Teiler hat: die Zahl 1 und sich selbst. Da die Zahl 1 nur einen Teiler hat (sich selbst), erfüllt sie nicht diese Definition und wird daher nicht als Primzahl betrachtet.
2. Teilbarkeitseigenschaften
Primzahlen haben spezielle Teilbarkeitseigenschaften, die ihnen ermöglichen, nur durch 1 und sich selbst ohne Rest teilbar zu sein. Die Zahl 1 erfüllt diese Eigenschaft nicht, da sie durch jede beliebige Zahl ohne Rest teilbar ist.
3. Einfluss auf Primfaktorzerlegung
Die Primfaktorzerlegung einer Zahl ist die Darstellung der Zahl als Produkt von Primzahlen. Da die Zahl 1 keine Primzahl ist, kann sie auch nicht in ihre Primfaktoren zerlegt werden. Die Primfaktorzerlegung der Zahl 1 wäre einfach nur „1“, was keinen weiteren mathematischen Nutzen hätte.
Daher gibt es mehrere Gründe, warum die Zahl 1 keine Primzahl ist und in der Mathematik eine besondere Stellung einnimmt.
Die Ausnahme der Zahl 1 in Bezug auf Primzahlen

Die Zahl 1 ist keine Primzahl
Die Zahl 1 ist eine Ausnahme in Bezug auf Primzahlen. Obwohl sie nur einen Teiler hat, nämlich sich selbst, wird sie nicht als Primzahl betrachtet. Eine Primzahl muss genau zwei Teiler haben, die 1 und die Zahl selbst. Da die Zahl 1 diese Bedingung nicht erfüllt, wird sie nicht als Primzahl angesehen.
Grund für die Nicht-Primzahl-Einstufung der Zahl 1
Der Grund dafür, dass die Zahl 1 nicht als Primzahl gilt, liegt darin, dass jede natürliche Zahl durch 1 teilbar ist. Wenn man die Definition von Primzahlen verwendet, würde dies bedeuten, dass jede natürliche Zahl eine Primzahl ist. Um Klarheit zu schaffen und das Konzept der Primzahlen eindeutig zu definieren, wurde beschlossen, die Zahl 1 von den Primzahlen auszuschließen.
Eigenschaften der Zahl 1
Die Zahl 1 hat einige einzigartige Eigenschaften. Sie ist weder eine Prime noch eine Composite-Zahl. Sie wird oft als „Einheit“ bezeichnet und spielt eine wichtige Rolle in mathematischen Operationen wie Multiplikation und Division. In vielen mathematischen Theorien wird die Einbeziehung der Zahl 1 in bestimmte Berechnungen oder Beweise erleichtert.
Zusammenfassend lässt sich sagen, dass die Zahl 1 aufgrund ihrer speziellen Eigenschaften und ihrer Abweichung von der Definition einer Primzahl nicht als Primzahl betrachtet wird.
Warum erfüllt die Zahl 1 nicht die Kriterien einer Primzahl?
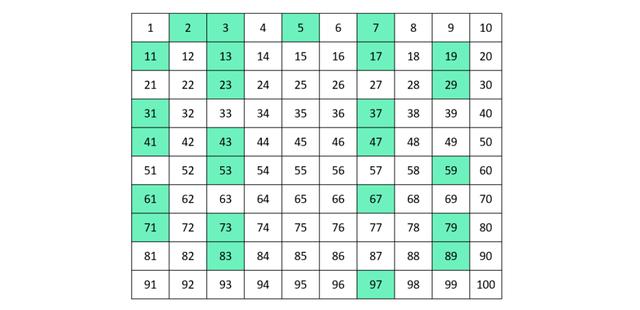
Die Zahl 1 hat nur einen Teiler
Die Zahl 1 erfüllt nicht die Kriterien einer Primzahl, da sie nur einen Teiler hat. Eine Primzahl hingegen hat genau zwei Teiler, nämlich die 1 und sich selbst. Da die Zahl 1 nur den Teiler 1 besitzt, kann sie keine Primzahl sein.
Primzahlen sind definiert als natürliche Zahlen größer als 1
Eine weitere Eigenschaft von Primzahlen ist, dass sie immer größer als 1 sein müssen. Die Zahl 1 erfüllt diese Bedingung nicht, da sie gleichzeitig kleiner als alle anderen natürlichen Zahlen ist. Daher wird die Zahl 1 nicht als Primzahl betrachtet.
Primzahlen haben spezielle Eigenschaften
Primzahlen haben einige besondere Eigenschaften, wie zum Beispiel dass sie nur durch sich selbst und durch 1 ohne Rest teilbar sind. Diese Eigenschaften treffen auf die Zahl 1 nicht zu, weshalb sie nicht als Primzahl angesehen wird.
Zusammenfassend kann man sagen, dass die Zahl 1 keine Primzahl ist, da sie nur einen Teiler hat und gleichzeitig kleiner als alle anderen natürlichen Zahlen ist.
Insgesamt lässt sich festhalten, dass die Zahl 1 keine Primzahl ist, da sie nur einen Teiler hat und nicht den Anforderungen einer Primzahl entspricht. Ihre Einzigartigkeit als kleinste natürliche Zahl macht sie zu einer Sonderstellung in der Mathematik. Die Eigenschaften von Primzahlen sind ein fundamentales Konzept, das in vielen mathematischen Bereichen Anwendung findet.

