Die Ableitung hat in der Mathematik eine wichtige Bedeutung. Erfahren Sie hier, was es mit der zweiten Ableitung auf sich hat und wie sie angewendet wird.
- Bedeutung des Synodalen Weges für die Kirche in Deutschland
- Die mystische Bedeutung der Sak Yant Tattoos: Eine spirituelle Tradition (82 characters)
- Sicherheitsmerkmale des Scheckkartenführerscheins 4a: Bedeutung und Erklärung
- Die spirituelle Bedeutung der Engelszahl 555 – Erfahre, warum siehst du 5:55?
- Tipps für lange Haltbarkeit: So bleiben Tulpen länger frisch
Die Bedeutung der zweiten Ableitung: Krümmung und Wendepunkte
Die zweite Ableitung einer Funktion gibt Aufschluss über deren Krümmung. Sie zeigt, ob der Graph der Funktion konkav (nach oben geöffnet) oder konvex (nach unten geöffnet) verläuft. Um dies zu verstehen, betrachten wir den Zusammenhang zwischen der zweiten Ableitung und Wendepunkten.
Ein Wendepunkt ist ein Punkt auf dem Graphen einer Funktion, an dem die Krümmungsrichtung wechselt. Das bedeutet, dass sich die Konkavität des Graphen von links nach rechts oder umgekehrt ändert. An einem Wendepunkt ist die Krümmung weder nach links noch nach rechts gerichtet.
Um einen möglichen Wendepunkt zu identifizieren, setzen wir den x-Wert des Punktes in die zweite Ableitung ein. Wenn die zweite Ableitung an dieser Stelle den Wert null ergibt, deutet dies auf einen möglichen Wendepunkt hin. Der Graph kann an diesem Punkt weder konkav noch konvex sein.
Es ist wichtig zu beachten, dass die zweite Ableitung keine Informationen über die Stärke der Krümmung liefert. Sie gibt lediglich Auskunft darüber, ob die Funktion konkav oder konvex verläuft. Die Stärke der Krümmung kann nur durch eine qualitative Betrachtung des Graphen beurteilt werden.
Zusammenfassend lässt sich sagen, dass die zweite Ableitung einer Funktion wichtige Informationen über deren Krümmung und mögliche Wendepunkte liefert. Sie ermöglicht es uns zu bestimmen, ob der Graph konkav oder konvex verläuft und wo mögliche Wendepunkte liegen könnten.
Die zweite Ableitung: Wert oder Funktion?
Die zweite Ableitung einer Funktion gibt Informationen über die Krümmung der Funktion an verschiedenen Stellen. Anders als die erste Ableitung, die die Steigung der Funktion beschreibt, sagt die zweite Ableitung nichts über die Stärke der Krümmung aus. Stattdessen gibt sie Auskunft darüber, ob die Funktion linksgekrümmt (konvex) oder rechtsgekrümmt (konkav) ist.
Um Informationen zur Krümmung an einer bestimmten Stelle zu erhalten, setzt man den entsprechenden x-Wert in die zweite Ableitung ein. Ist der Wert der zweiten Ableitung kleiner als null, bedeutet das, dass die Funktion rechtsgekrümmt ist. Ist er größer als null, ist die Funktion linksgekrümmt. Wenn der Wert genau null ist, kann dies auf einen möglichen Wendepunkt oder Sattelpunkt hinweisen.
Es ist wichtig zu beachten, dass die zweite Ableitung nicht alleine betrachtet werden sollte. Sie sollte immer in Verbindung mit der ersten Ableitung analysiert werden. Wenn sowohl die erste als auch die zweite Ableitung an einem Punkt null sind, kann dies auf einen möglichen Sattelpunkt hindeuten. Wenn jedoch die erste Ableitung an einem Punkt null ist und die zweite Ableitung positiv (größer als null), handelt es sich wahrscheinlich um einen Tiefpunkt. Ist hingegen die erste Ableitung null und die zweite negativ (kleiner als null), kann es sich um einen Hochpunkt handeln.
Insgesamt liefert uns also die Analyse der ersten und zweiten Ableitungen wichtige Informationen über den Verlauf und Charakter einer Funktion.
Zusammenhang zwischen erster und zweiter Ableitung
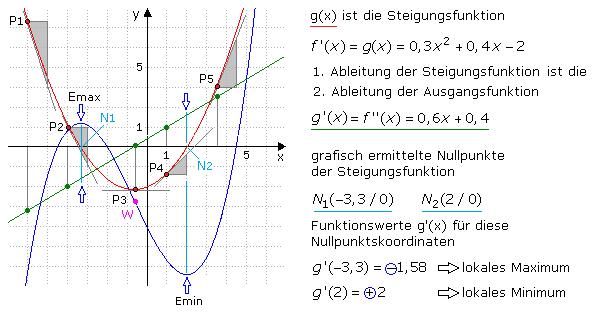
Die erste Ableitung einer Funktion gibt uns Informationen über die Steigung dieser Funktion. Sie zeigt uns, wie schnell sich der Funktionswert ändert, wenn sich der Wert der unabhängigen Variable verändert. Wenn die erste Ableitung an einer bestimmten Stelle positiv ist, bedeutet dies, dass die Funktion an dieser Stelle steigt. Ist die Ableitung negativ, fällt die Funktion an dieser Stelle.
Die zweite Ableitung einer Funktion gibt uns Informationen über die Krümmung dieser Funktion. Sie zeigt uns, wie stark sich die Steigung der Funktion ändert. Die zweite Ableitung kann sowohl positiv als auch negativ sein. Ist sie positiv, bedeutet dies, dass die Funktion eine konvexe Krümmung hat und nach oben geöffnet ist. Ist sie negativ, hat die Funktion eine konkave Krümmung und ist nach unten geöffnet.
Der Zusammenhang zwischen erster und zweiter Ableitung besteht darin, dass die erste Ableitung aus der zweiten Ableitung abgeleitet werden kann. Das heißt, wenn wir den Wert der zweiten Ableitung kennen und diesen in die Formel für die erste Ableitung einsetzen, erhalten wir den Wert der ersten Ableitung an dieser Stelle.
Ein weiterer Zusammenhang besteht zwischen Extrempunkten (Hoch- oder Tiefpunkten) einer Funktion und ihrer ersten und zweiten Ableitungen. Wenn der Wert der ersten Ableitung an einem Extrempunkt Null ist und die zweite Ableitung negativ ist, handelt es sich um einen Hochpunkt. Ist hingegen die zweite Ableitung positiv, haben wir es mit einem Tiefpunkt zu tun. Wenn sowohl erste als auch zweite Ableitung an einem Punkt null sind, handelt es sich um einen möglichen Sattelpunkt.
Zusammenfassend lässt sich sagen, dass die erste Ableitung einer Funktion Informationen über deren Steigung liefert, während die zweite Ableitung Informationen über deren Krümmung gibt. Der Zusammenhang zwischen erster und zweiter Ableitung ermöglicht es uns, weitere Eigenschaften der Funktion wie Extrempunkte zu bestimmen.
Krümmung und Richtung: Die Rolle der zweiten Ableitung
Die zweite Ableitung einer Funktion spielt eine wichtige Rolle bei der Analyse ihrer Krümmung und Richtung. Sie gibt Auskunft darüber, wie sich die Krümmung der Funktion an verschiedenen Stellen verändert.
Ein wichtiger Unterschied zur ersten Ableitung besteht darin, dass die zweite Ableitung keinen konkreten Wert für die Krümmung liefert, sondern vielmehr Informationen über deren Richtung. Wenn die zweite Ableitung den Wert 0 hat, kann dies auf das Vorhandensein eines Wendepunktes oder eines Sattelpunktes hinweisen. In diesem Fall ändert sich die Krümmung der Funktion von links nach rechts oder umgekehrt.
Die Form des Graphen einer Funktion kann ebenfalls Aufschluss über ihre Krümmung geben. Wenn der Graph eher talförmig ist (wie ein „u“), spricht man von einer linkskrümmenden Funktion, auch als konvex bezeichnet. Ist der Graph hingegen eher bergförmig, handelt es sich um eine rechtskrümmende Funktion, auch konkav genannt.
Um weitere Informationen über einen Extrempunkt zu erhalten, kann man den x-Wert dieses Punktes in die zweite Ableitung einsetzen. Dadurch erhält man zusätzliche Details zu diesem Punkt.
Es ist wichtig anzumerken, dass die Stärke der Krümmung nicht durch die zweite Ableitung bestimmt wird. Diese gibt lediglich Auskunft über Richtungsänderungen in Bezug auf die Krümmung.
Zusammenfassend lässt sich sagen, dass die zweite Ableitung einer Funktion wichtige Informationen über ihre Krümmung und Richtung liefert. Sie kann Hinweise auf Wendepunkte, Sattelpunkte und die Art der Krümmung geben. Die erste Ableitung ist eng mit der zweiten Ableitung verbunden und kann durch Ableiten der Funktion gewonnen werden.
Wende- und Sattelpunkte: Was die zweite Ableitung verrät
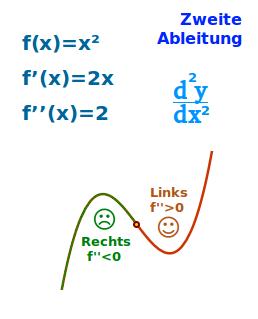
Ein wichtiger Unterschied zwischen der ersten und zweiten Ableitung besteht darin, dass die erste Ableitung Informationen über die Steigung der Funktion gibt, während die zweite Ableitung etwas über die Krümmung aussagt.
Die zweite Ableitung einer Funktion f(x), auch als f“(x) bezeichnet, kann an bestimmten Stellen den Wert 0 haben. An diesen Stellen können sich Wende- oder Sattelpunkte befinden oder die Funktion verläuft linear (gerade). Die zweite Ableitung gibt jedoch keine Auskunft über die Stärke der Krümmung.
Die Richtung der Krümmung kann durch den Graphen der Funktion visualisiert werden. Wenn der Graph eher talförmige Formen aufweist und nach unten geöffnet ist (wie ein „u“), ist er linksgekrümmt oder konvex. Wenn der Graph eher bergförmig ist und nach oben geöffnet ist, ist er rechtsgekrümmt oder konkav.
Um weitere Informationen zu einem Extrempunkt zu erhalten, kann man den x-Wert des Punktes in die zweite Ableitung einsetzen. An diesem Punkt wechselt die Krümmung von links nach rechts oder umgekehrt. Der Graph selbst ist weder links- noch rechtsgekrümmt an dieser Stelle.
Es gibt auch eine Beziehung zwischen der ersten und zweiten Ableitung. Die erste Ableitung f'(x) abgeleitet ergibt die zweite Ableitung f“(x). Durch das Einsetzen eines x-Wertes in die erste Ableitung erhält man den Wert der zweiten Ableitung.
Zusammenfassend lässt sich sagen, dass die zweite Ableitung einer Funktion wichtige Informationen über Wende- und Sattelpunkte liefert. Sie gibt Auskunft darüber, ob die Funktion linksgekrümmt, rechtsgekrümmt oder weder noch ist. Die erste Ableitung hingegen gibt Informationen über die Steigung der Funktion.
Der Einfluss der zweiten Ableitung auf die Form der Funktion
Die zweite Ableitung einer Funktion hat einen entscheidenden Einfluss auf deren Form. Sie gibt Auskunft über die Krümmung des Graphen und ermöglicht es, Wende- und Sattelpunkte zu identifizieren.
1. Die Krümmung des Graphen
Die zweite Ableitung f“(x) einer Funktion f(x) gibt Informationen über die Krümmung des Graphen an verschiedenen Stellen wieder. Wenn die zweite Ableitung den Wert 0 hat, kann dies auf das Vorliegen eines Wende- oder Sattelpunktes hinweisen. An diesen Punkten wechselt die Krümmung von links nach rechts oder umgekehrt. Der Graph ist weder links- noch rechtsgekrümmt an diesen Stellen.
Wenn die zweite Ableitung positiv ist (f“(x) > 0), ist der Graph linkskrümmt oder konkav. Dies bedeutet, dass er eher talförmige Formen annimmt, ähnlich einem „u“.
Wenn hingegen die zweite Ableitung negativ ist (f“(x) < 0), ist der Graph rechtskrümmt oder konvex. Er hat eine eher bergförmige Form.
2. Wende- und Sattelpunkte
Die zweite Ableitung ermöglicht es auch, Wende- und Sattelpunkte einer Funktion zu bestimmen. Wenn man den x-Wert eines Extrempunktes in die zweite Ableitung einsetzt, erhält man weitere Informationen zu diesem Punkt.
Wenn die erste Ableitung f'(x) an einem Punkt Null ist und die zweite Ableitung f“(x) negativ ist, handelt es sich um einen Hochpunkt. Der Graph steigt vor dem Punkt an und fällt danach ab.
Wenn die erste Ableitung f'(x) an einem Punkt Null ist und die zweite Ableitung f“(x) positiv ist, handelt es sich um einen Tiefpunkt. Der Graph fällt vor dem Punkt ab und steigt danach an.
Wenn sowohl die erste als auch die zweite Ableitung an einem Punkt Null sind, kann es sich um einen Sattelpunkt handeln. An dieser Stelle wechselt der Graph seine Krümmung von links nach rechts oder umgekehrt.
Die zweite Ableitung einer Funktion spielt also eine wichtige Rolle bei der Bestimmung ihrer Form und ermöglicht es, verschiedene Eigenschaften wie Krümmung, Wende- und Sattelpunkte zu analysieren.
Die Ableitung ist ein wichtiges Konzept in der Mathematik, das die Änderungsrate einer Funktion beschreibt. Sie spielt eine entscheidende Rolle in vielen Bereichen wie Physik, Wirtschaft und Ingenieurwesen. Die Fähigkeit, Ableitungen zu berechnen und zu interpretieren, ermöglicht es uns, komplexe Probleme zu lösen und Zusammenhänge besser zu verstehen. Die Bedeutung der Ableitung kann daher nicht unterschätzt werden.